12 Using R to compute probabilities

For most probability distributions, R has 4 built-in functions that tell you almost everything you will ever want to know about them.

For the Binomial distribution, these functions are the following:

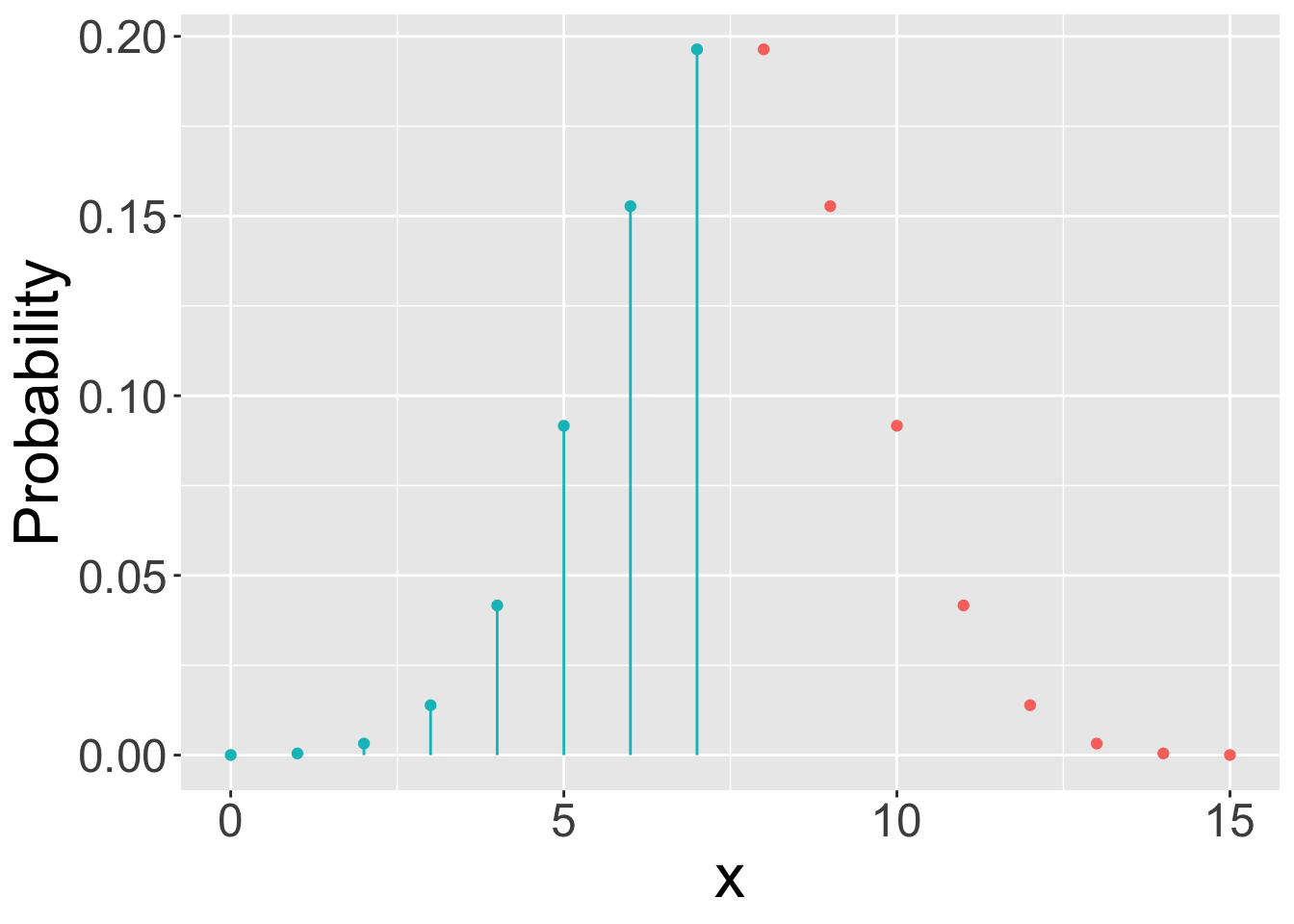
  • dbinom(x): Probability mass function
  • pbinom(x): Cumulative distribution function
  • qbinom(p): quantile function
  • rbinom(n): function for random samples

For the Normal distributions, these functions are the following:

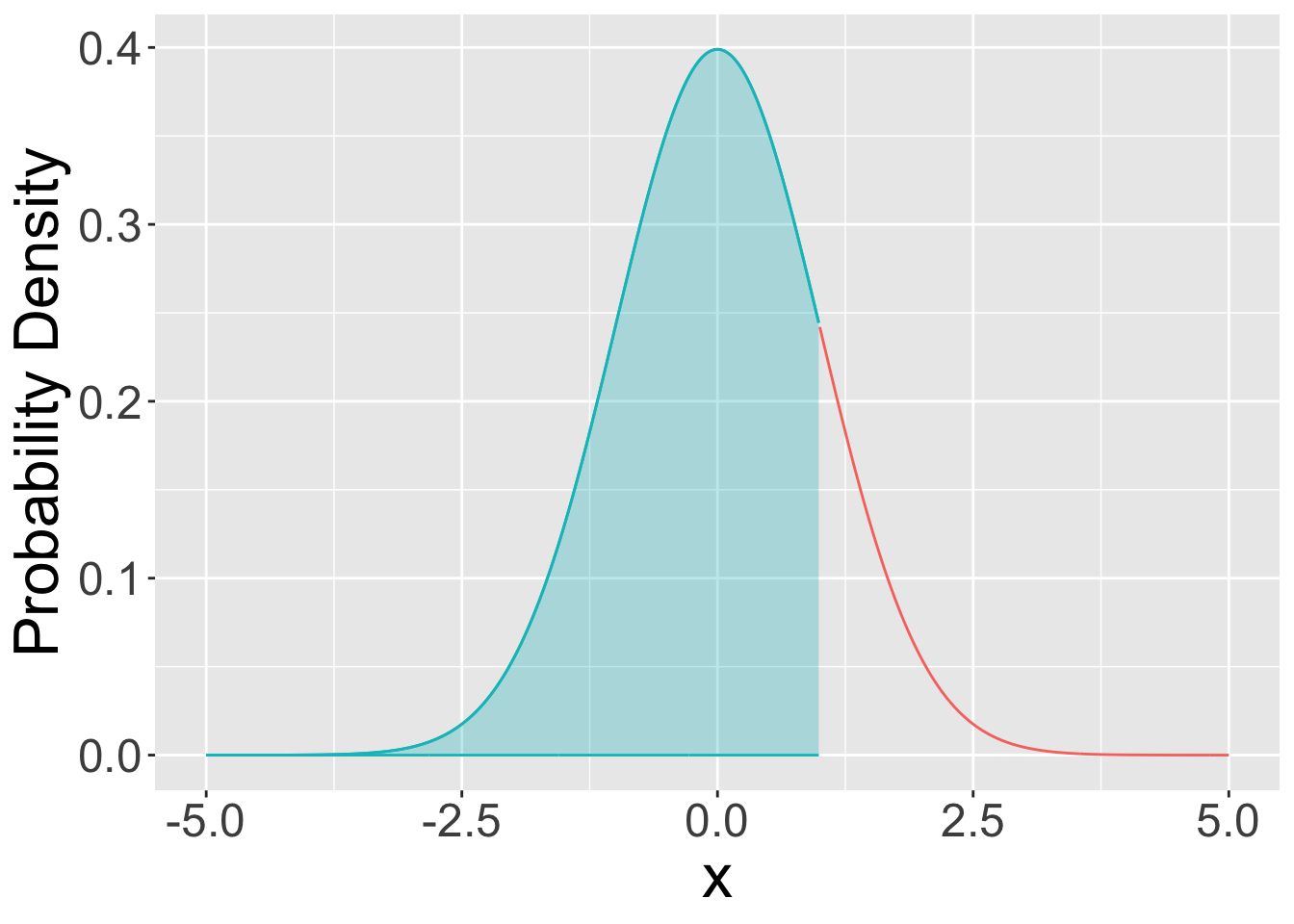
  • dnorm(x): Probability density function
  • pnorm(x): Cumulative distribution function
  • qnorm(p): quantile function
  • rnorm(n): function for random samples

You can see the naming convention adopted by R right away.

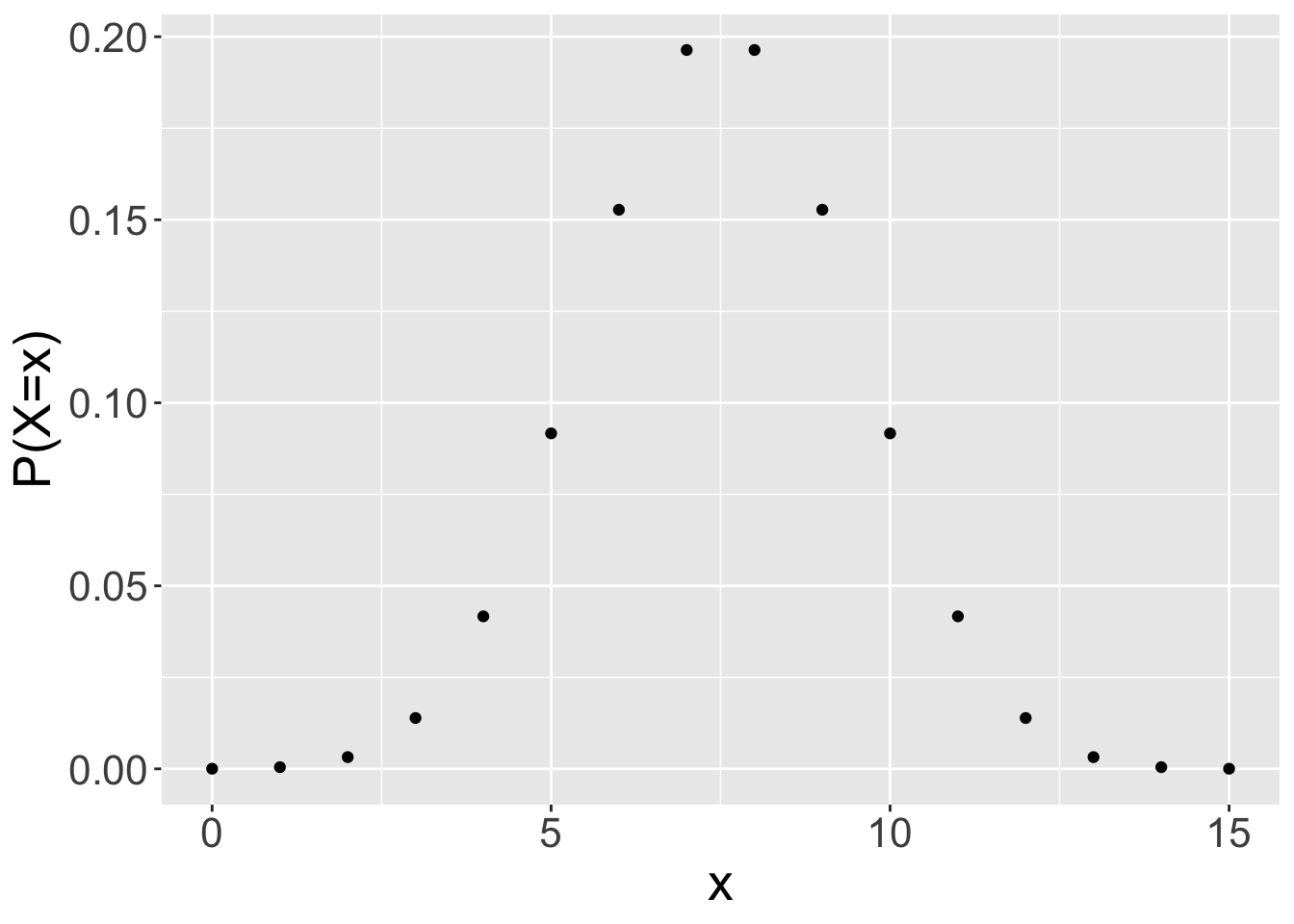
  • The d functions are mass or density functions.

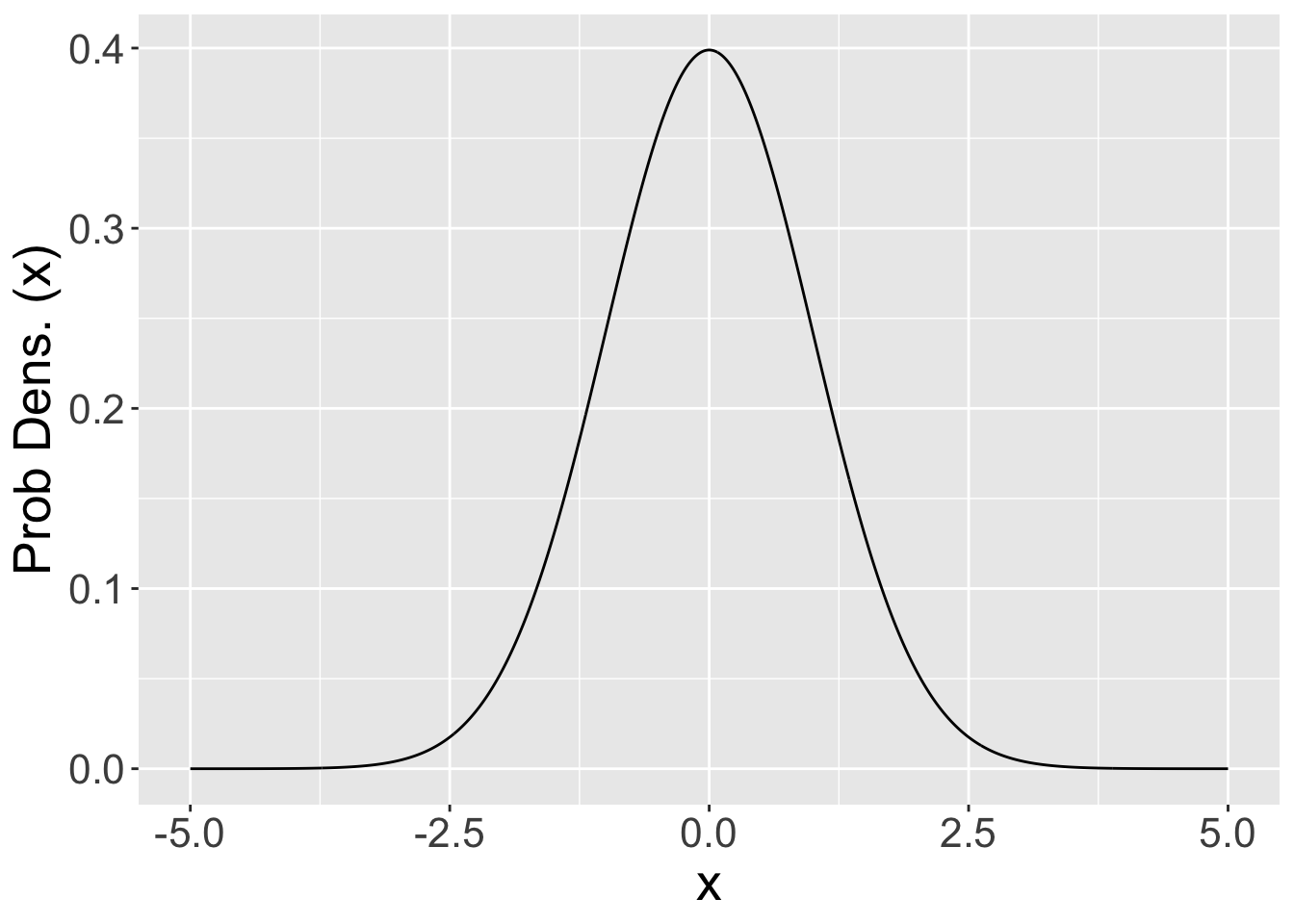
    • For discrete distributions, these functions return \(P(X=x)\). E.g., dbinom(x, n, p) returns the probability that a binomial random variable with parameters \(n\) and \(p\) will yield a value of \(x\).

    • For continuous distributions, these functions return a probability density. To get probability, we must consider a range of outcomes \([a, b]\) and compute the area under the curve. Computing the exact area under the curve requires evaluating an integral, which is too hard for us and awkward to do using a d function. It will be best to use a p function in this case (see below).

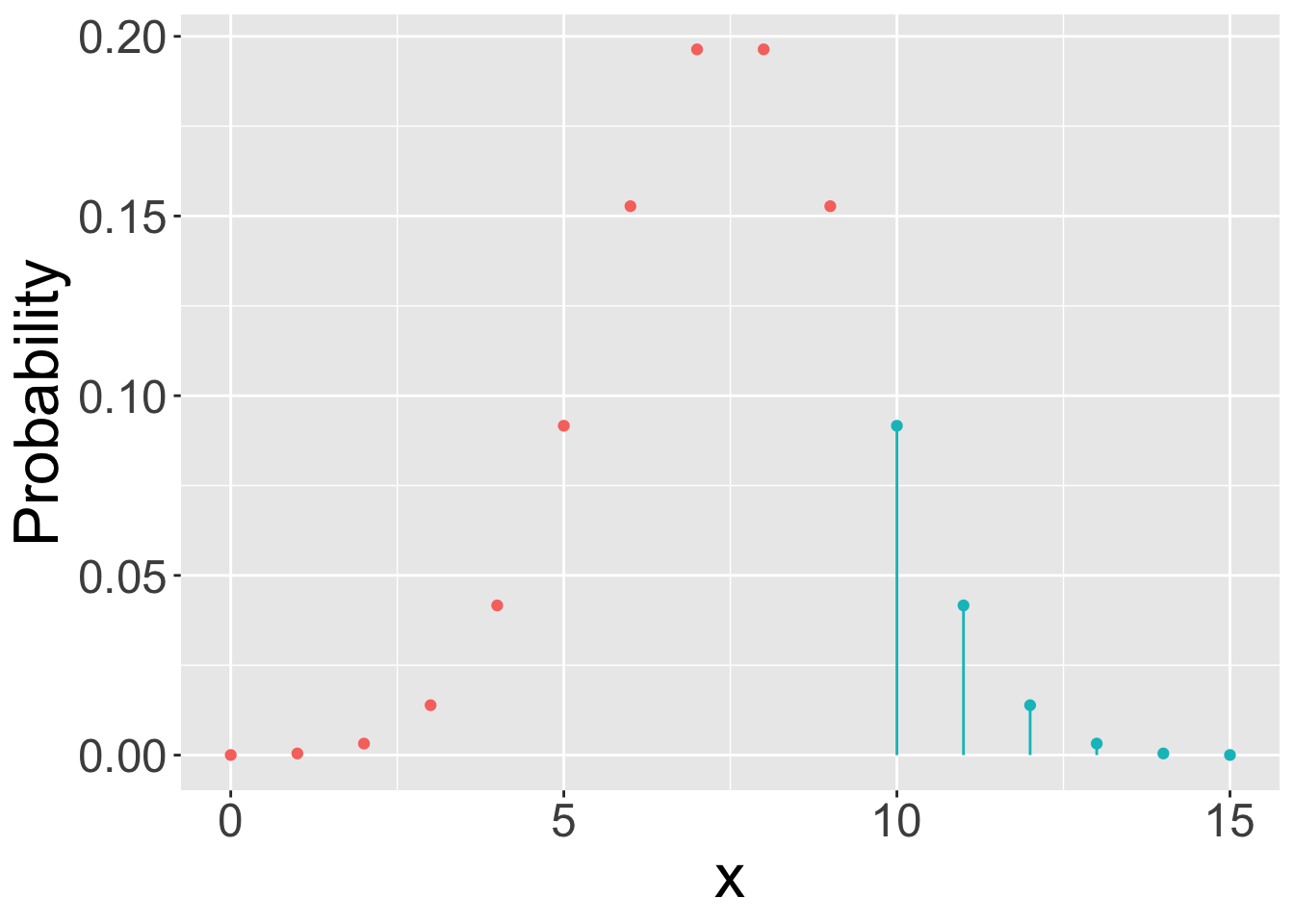
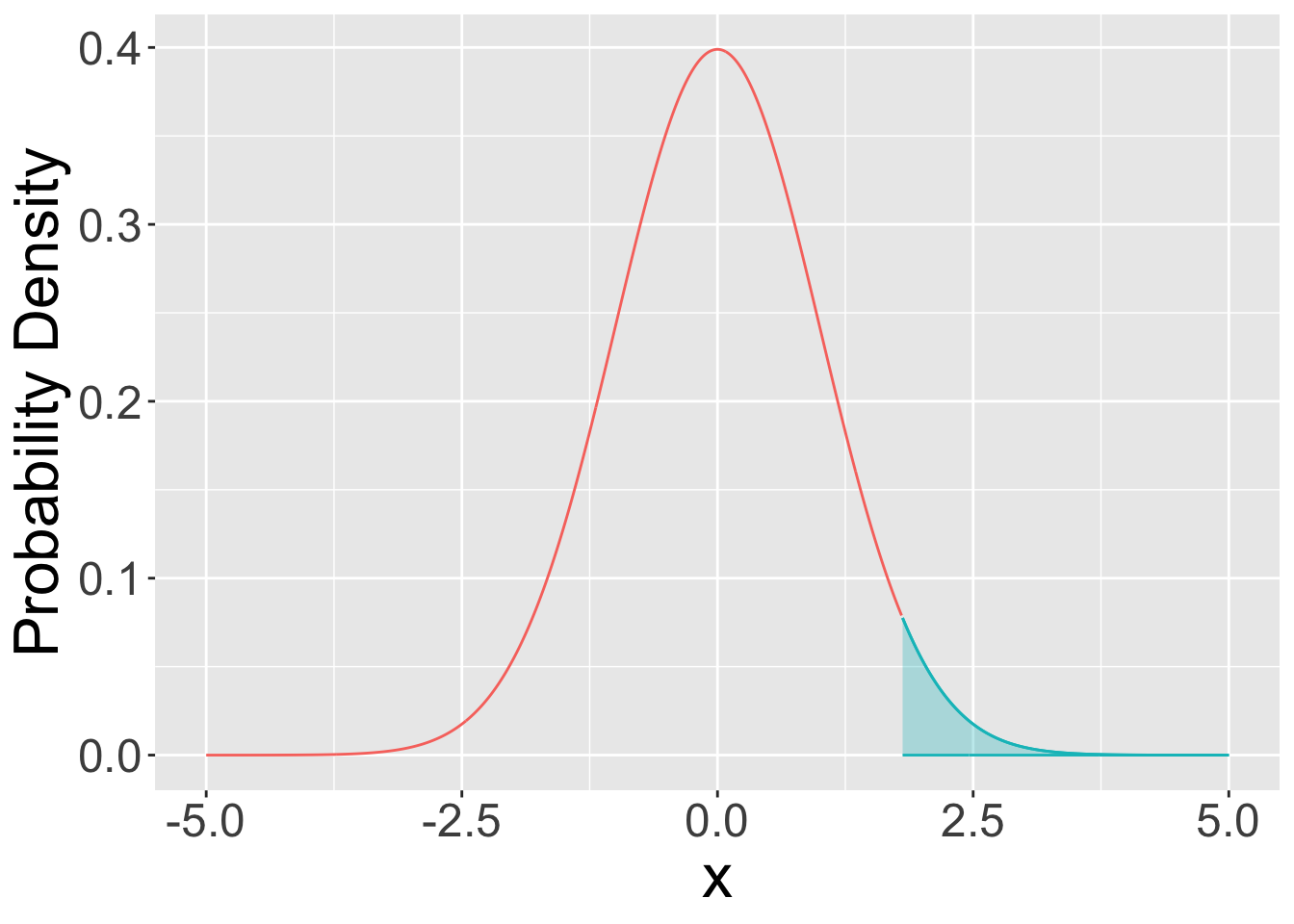
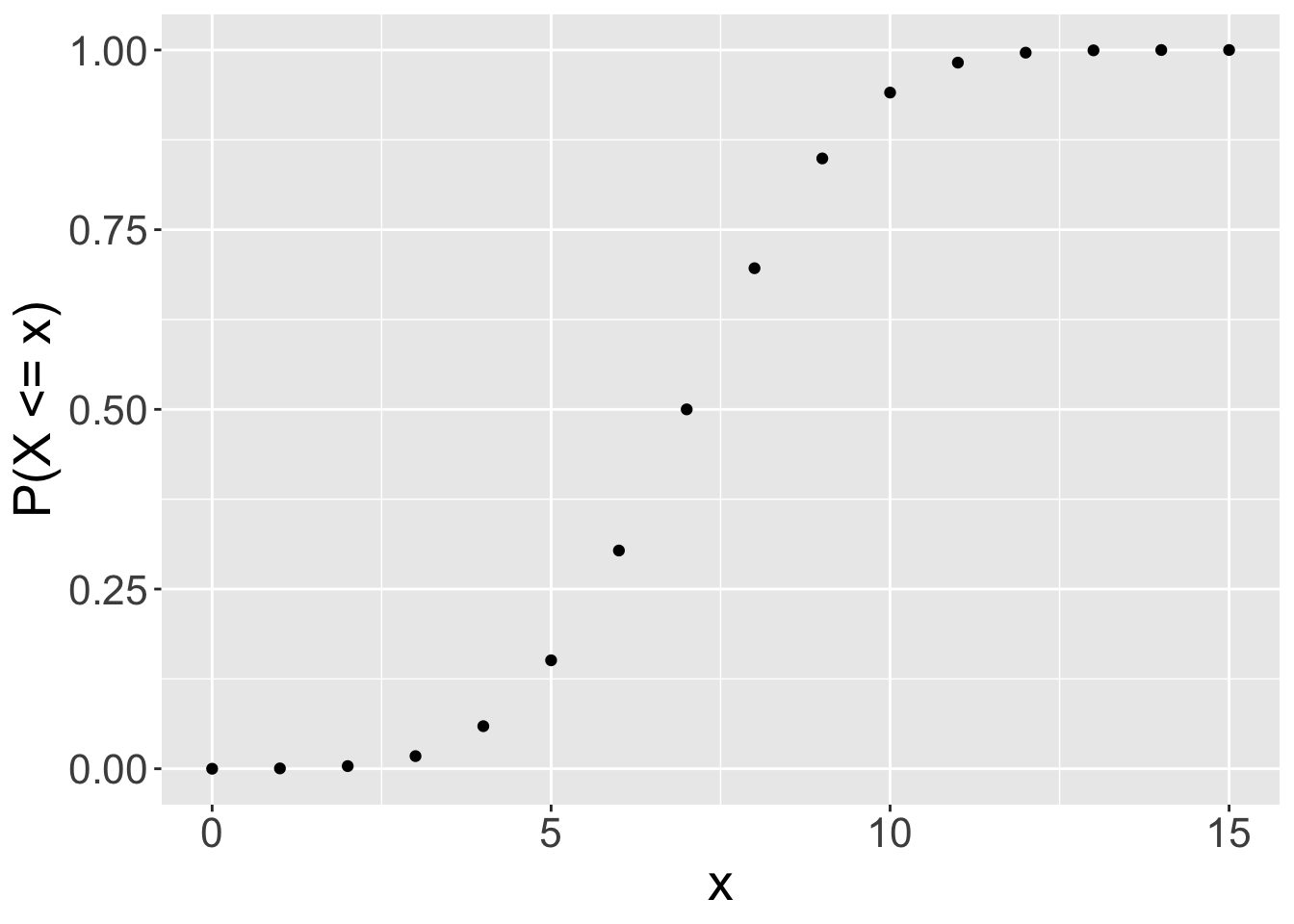
  • The p functions are cumulative probability functions.

    • By default these functions return \(P(X \leq x)\). If you specify lower.tail=FALSE then these functions return \(P(X\>x)\). Be careful when using these functions to appreciate that for continuous distributions \(P(X \leq x)=1-P(X \geq x)\) but for discrete distributions \(P(X \leq x)=1-P(X \geq x+1)\). All that is basically just to say be careful when considering whether to use greater than or greather than and equal to etc.

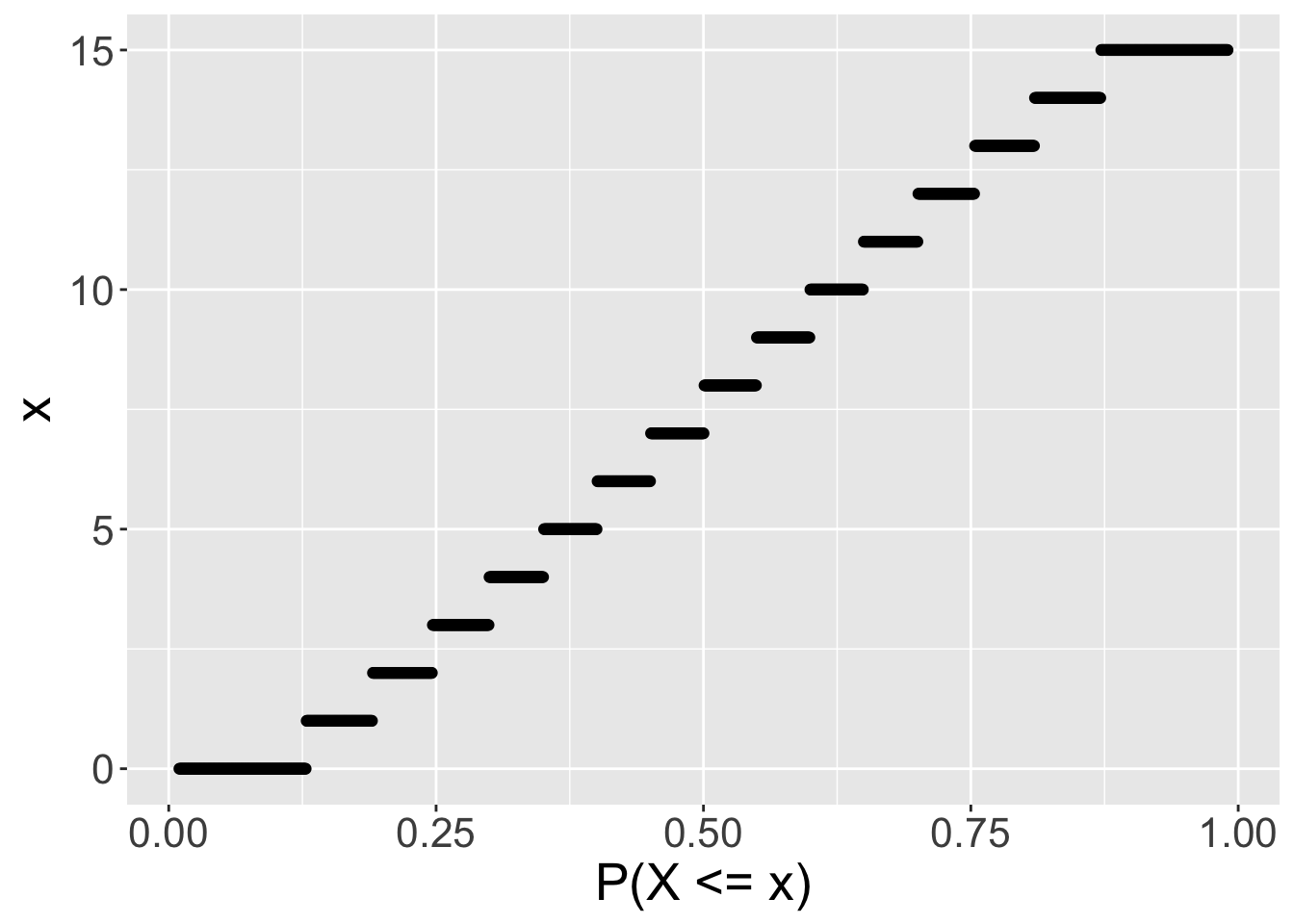
  • The q functions are quantile functions.

    • They are the inverse of the cumulative probability functions. Here, you specify a cumulative probability \(q\), and the function returns the value of \(x\) such that \(P(X\<x)=q\).

  • The r functions generate random samples.

pmf: probabilities are given by values on the y-axis.

cdf: cumulative probabilities \((X\<x)\) are given by reading values on the y-axis.

qf: use this function to specify a probability (x-axis) and get the value that satisfies this probability from the y-axis.

pdf: probabilities are given by the area under the curve.

cdf: cumulative probabilities \((X\<x)\) are given by reading values on the y-axis.

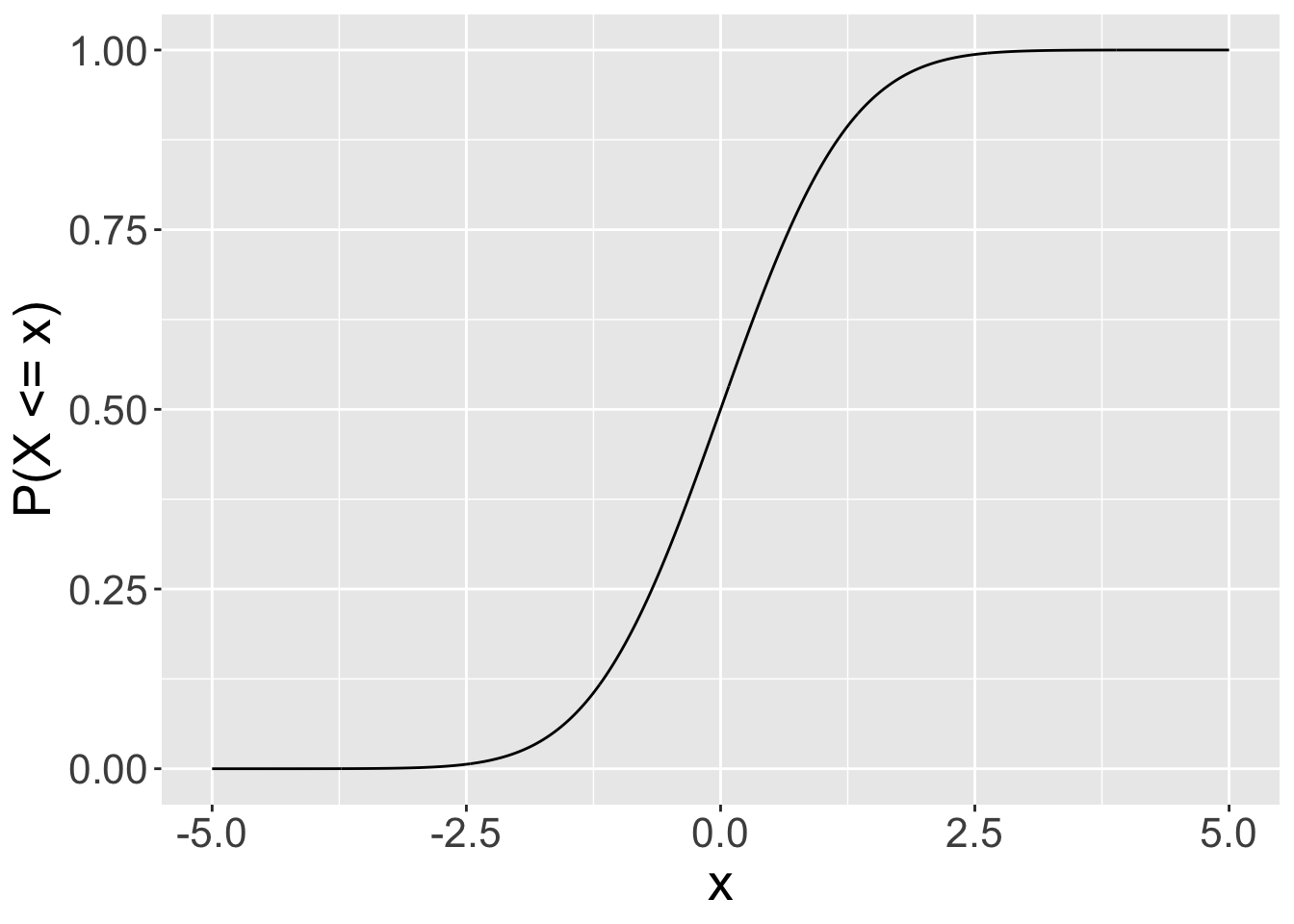
qf: use this function to specify a probability (x-axis) and get the value that satisfies this probability from the y-axis.

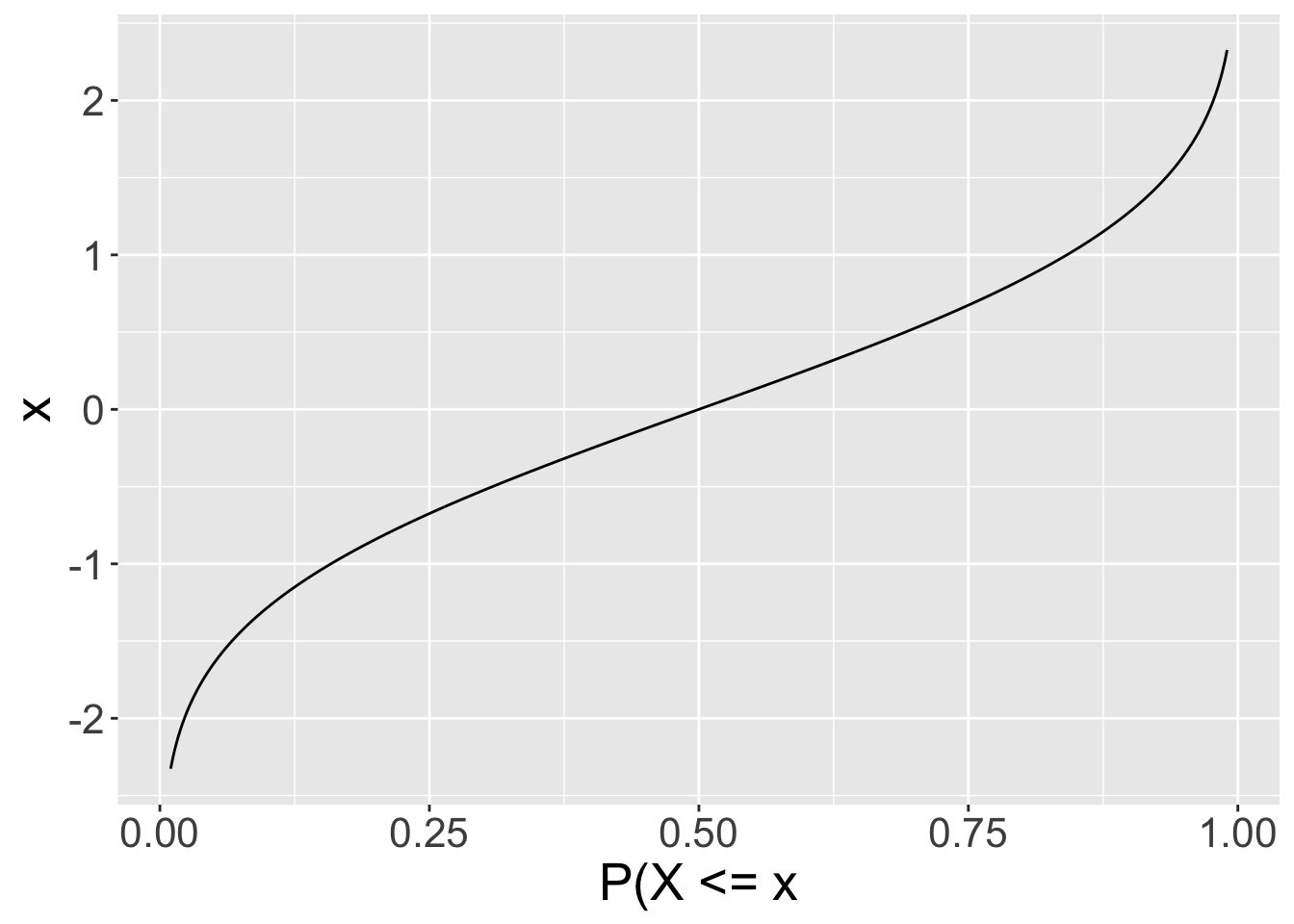
In general, I think it is important for you to be able to read each of the types of plots above, so please really try to encode these and think about them deeply.

12.0.0.1 Binomial example: \(P(X \< 8)\)

n <- 15
p <- 0.5

## Using pmf (exact)
px <- sum(dbinom(0:7, n, p))
px
## [1] 0.5
## using cdf (exact)
px <- pbinom(7, n, p)
px
## [1] 0.5

12.0.0.2 Normal example: \(P(X \< 1)\)

mu <- 0
sig <- 1

## Using pdf (not exact)
px <- sum(dnorm(seq(-5, 1, .1), mu, sig)*.1)
px
## [1] 0.8532414
## using cdf (exact)
px <- pnorm(1, mu, sig)
px
## [1] 0.8413447

12.0.0.3 Binomial example: \(P(X \> 9)\)

n <- 15
p <- 0.5

## Using pmf (exact)
px <- sum(dbinom(10:n, n, p))
px
## [1] 0.1508789
## using cdf (exact)
px <- pbinom(9, n, p, lower.tail=F)
px
## [1] 0.1508789

12.0.0.4 Normal example: \(P(X \> 1.8)\)

mu <- 0
sig <- 1

## Using pdf (not exact)
p <- sum(dnorm(seq(1.8, 5, .1), mu, sig)*.1)
p
## [1] 0.03999603
## using cdf (exact)
p <- pnorm(1.8, mu, sig, lower.tail=F)
p
## [1] 0.03593032