30 General linear model (GLM)
30.1 General linear model: ANOVA and regression have a common base
- The multiple regression model we just considered is an example of the general linear model.
\[\begin{align} y_{i} &= \beta_{0} + \beta_{1} x_{1_i} + \beta_{2} x_{2_i} + \dots + \beta_{k} x_{k_i} + \epsilon_{i} \\\\ \boldsymbol{y} &= \beta_{0} \begin{bmatrix} 1\\ 1\\ \vdots\\ 1 \end{bmatrix} + \beta_{1} \begin{bmatrix} x_{1_1}\\ x_{1_2}\\ \vdots\\ x_{1_n}\\ \end{bmatrix} + \beta_{2} \begin{bmatrix} x_{2_1}\\ x_{2_2}\\ \vdots\\ x_{2_n}\\ \end{bmatrix} + \ldots + \beta_{k} \begin{bmatrix} x_{k_1}\\ x_{k_2}\\ \vdots\\ x_{k_n}\\ \end{bmatrix} + \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n\\ \end{bmatrix} \\\\ \boldsymbol{y} &= \begin{bmatrix} 1 & x_{1_1} & x_{2_1} & \ldots & x_{k_1} \\ 1 & x_{1_2} & x_{2_2} & \ldots & x_{k_2} \\ \vdots & \vdots & \dots & \dots \\ 1 & x_{1_n} & x_{2_n} & \ldots & x_{k_n} \end{bmatrix} \begin{bmatrix} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{k} \end{bmatrix} + \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n\\ \end{bmatrix} \\\\ \boldsymbol{y} &= \boldsymbol{X} \boldsymbol{\beta} + \boldsymbol{\epsilon} \end{align}\]
In regression, the \(x_{i,j}\) values that make up the design matrix \(\boldsymbol{X}\) – i.e., the regressors – are continuously valued.
ANOVA can be framed by exactly the same linear model, given that the ANOVA factors are input as “dummy coded” regressors.
What is dummy coding? Consider a factor with three levels. We can dummy code this as follows:
| Factor level | Dummy variable 1 | Dummy variable 2 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0 |
| 3 | 0 | 1 |
- This coding leads to the following linear model:
\[\begin{align} \boldsymbol{y} &= \beta_{0} \begin{bmatrix} 1\\ 1\\ \vdots\\ 1\\ 1\\ \vdots\\ 1\\ 1\\ \end{bmatrix} + \beta_{1} \begin{bmatrix} 0\\ 0\\ \vdots\\ 1\\ 1\\ \vdots\\ 0\\ 0 \end{bmatrix} + \beta_{2} \begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 0\\ \vdots\\ 1\\ 1 \end{bmatrix} + \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_{m-1}\\ \epsilon_m\\ \vdots\\ \epsilon_{n-1}\\ \epsilon_n \end{bmatrix} \\\\ \boldsymbol{y} &= \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ \vdots & \vdots & \vdots\\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ \vdots & \vdots & \vdots\\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \beta_{0} \\ \beta_{1} \\ \beta_{2} \end{bmatrix} + \begin{bmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_{m-1}\\ \epsilon_m\\ \vdots\\ \epsilon_{n-1}\\ \epsilon_n\\ \end{bmatrix} \\\\ \boldsymbol{y} &= \boldsymbol{X} \boldsymbol{\beta} + \boldsymbol{\epsilon} \end{align}\]
- With this coding, it’s fairly straight forward to show the following:
\[ \beta_0 = \bar{x_1} \\ \beta_1 = \bar{x_2} - \bar{x_1} \\ \beta_2 = \bar{x_3} - \bar{x_1} \\ \]
- That is, the \(\beta\) estimates corresponds to differences in means, which is exactly what ANOVA is after.
30.1.0.1 Example: Criterion learning data
d <- fread('https://crossley.github.io/book_stats/data/criterion_learning/crit_learn.csv')
## We will answer this question: Are there significant differences between the
## mean `t2c` per subject betweem conditions? For simplicity, only consider the
## `Delay`, `Long ITI` and `Short ITI` conditions.
## clean up the data (just trsut me this makes sense to do here)
dd <- unique(d[prob_num <= 3 &
nps >= 3 &
cnd %in% c('Delay', 'Long ITI', 'Short ITI'),
.(cnd, sub, prob_num, t2c)])
ddd <- dd[, .(t2c=mean(t2c)), .(cnd, sub)]
ddd[, sub := factor(sub)]
ddd[, cnd := factor(cnd)]
ggplot(ddd, aes(x=cnd, y=t2c)) +
geom_boxplot() +
theme(legend.position='none')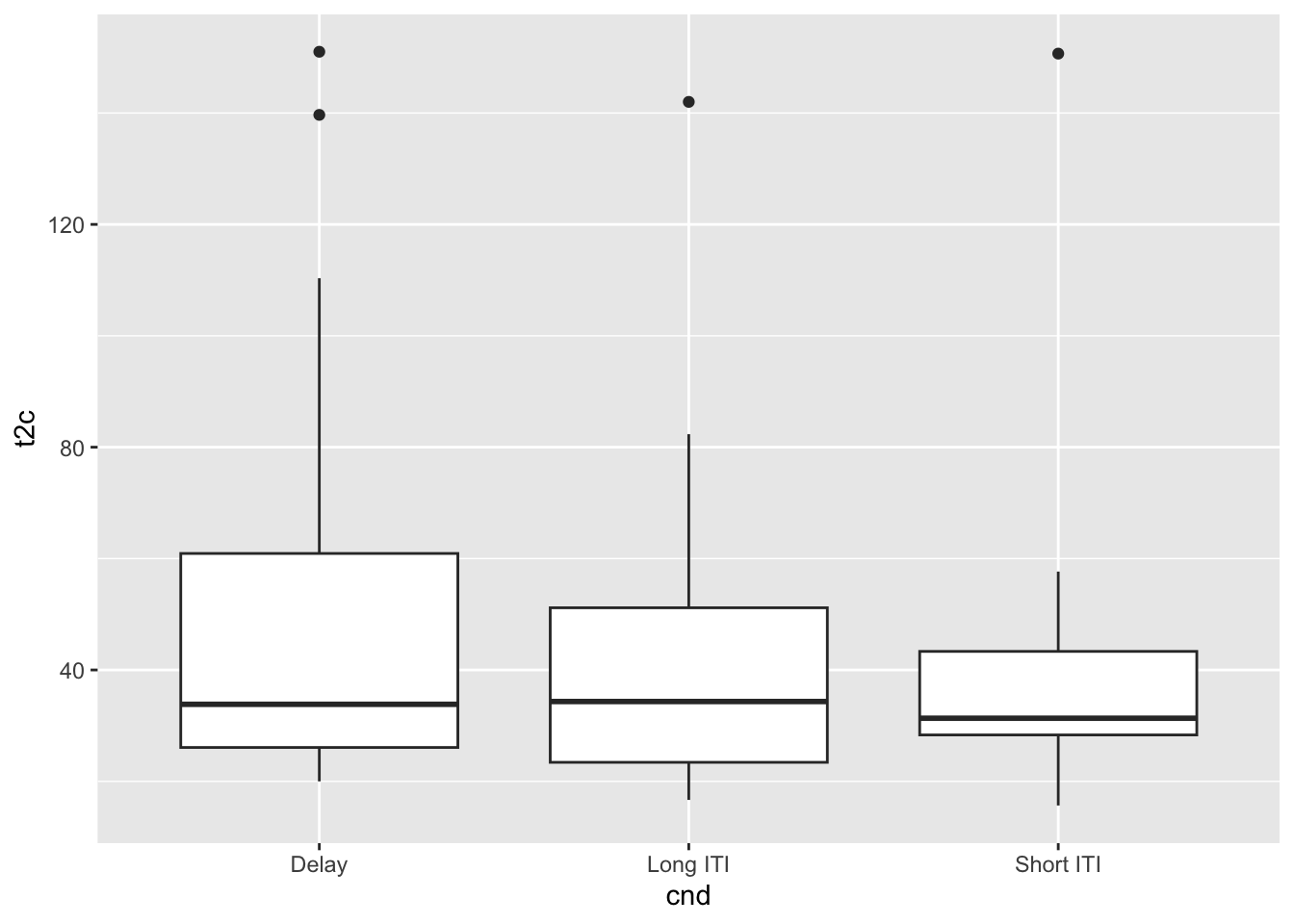
##
## Call:
## lm(formula = t2c ~ cnd, data = ddd)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.593 -21.259 -12.481 7.519 106.949
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.708 5.109 9.142 6.52e-12 ***
## cnd1 5.884 7.017 0.839 0.406
## cnd2 -2.894 7.017 -0.412 0.682
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 35.35 on 46 degrees of freedom
## Multiple R-squared: 0.01518, Adjusted R-squared: -0.02764
## F-statistic: 0.3544 on 2 and 46 DF, p-value: 0.7035## Analysis of Variance Table
##
## Response: t2c
## Df Sum Sq Mean Sq F value Pr(>F)
## cnd 2 886 442.82 0.3544 0.7035
## Residuals 46 57475 1249.45## [1] 52.59259## [1] -8.777778## [1] -8.874644Cool that we can see that R does the dummy coding for us, and automatically sets the baseline value to the
Delaycondition.What if you want to assign a different condition to baseline? Not for this lecture but you should keep taking classes and learning!
In summary, an regression with dummy coded factors as regressors is equivalent to an ANOVA, and both are just instances of the general linear model.