7 Hodgkin-Huxley neuron model

import numpy as np
import matplotlib.pyplot as plt

7.1 neuron_func_1

def neuron_func_1():
    '''
    NOTE: dvdt = I - g * (v - E)
    - has stable eq at E
    - looks reasonable for sub threshold dynamics
    - nothing like an action potential
    '''
    tau = 0.01
    T = 100
    t = np.arange(0, T, tau)
    n = t.shape[0]

    I = np.zeros(n)
    v = np.zeros(n)

    vr = -65.0
    E = -65.0
    g = 1.0
    C = 1.0

    v[0] = vr
    I[n // 5:2 * n // 5] = 30.0
    I[3 * n // 5:4 * n // 5] = -30.0

    for i in range(1, n):
        delta_t = t[i] - t[i - 1]
        dvdt = (I[i - 1] - g * (v[i - 1] - E)) / C
        v[i] = v[i - 1] + dvdt * delta_t

    fig, ax = plt.subplots(3, 1, squeeze=False)
    ax[0, 0].plot(t, I, label='I')
    ax[1, 0].plot(t, g * (v - E), label='g * (v - E)')
    ax[2, 0].plot(t, v, label='v')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()
    
neuron_func_1()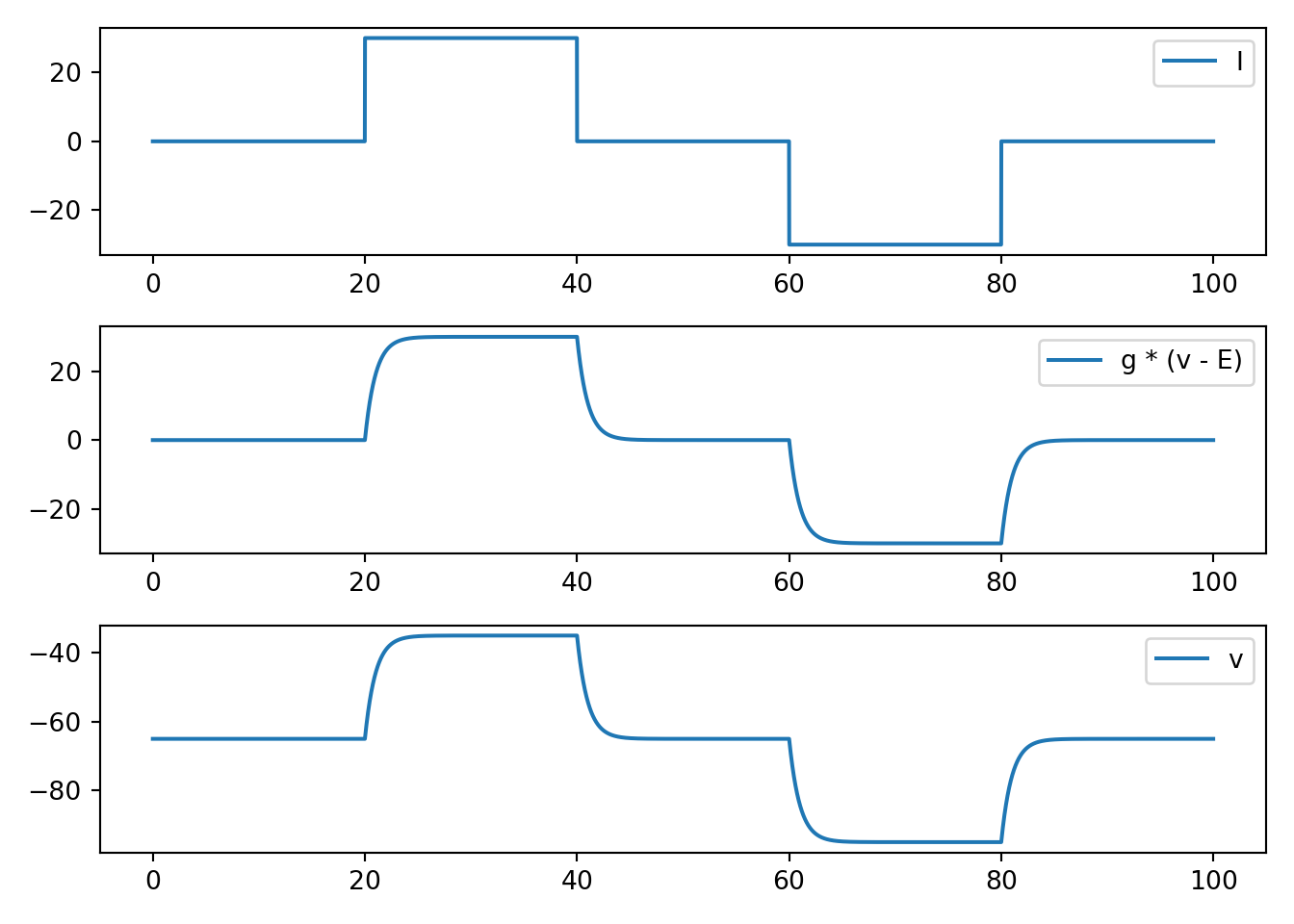

7.2 neuron_func_2

def neuron_func_2():
    '''
    NOTE: dvdt = I - g_a * (v - E_a) - g_b * (v - E_b)
    - has stable eq between E_a and E_b with balance determined by relative g's
    - still looks reasonable for sub threshold
    - still nothing like an action potential
    '''
    tau = 0.01
    T = 100
    t = np.arange(0, T, tau)
    n = t.shape[0]

    I = np.zeros(n)
    v = np.zeros(n)

    vr = -65.0
    E_a = -65.0
    E_b = 65.0
    g_a = 1.0
    g_b = 1.0
    C = 1.0

    v[0] = vr
    I[n // 5:2 * n // 5] = 30.0
    I[3 * n // 5:4 * n // 5] = -30.0

    for i in range(1, n):
        delta_t = t[i] - t[i - 1]
        dvdt = (I[i - 1] - g_a * (v[i - 1] - E_a) - g_b * (v[i - 1] - E_b)) / C
        v[i] = v[i - 1] + dvdt * delta_t

    fig, ax = plt.subplots(3, 1, squeeze=False)
    ax[0, 0].plot(t, I, label='I')
    ax[1, 0].plot(t, g_a * (v - E_a), label='g * (v - E)')
    ax[1, 0].plot(t, g_b * (v - E_b), label='g * (v - E)')
    ax[2, 0].plot(t, v, label='v')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()
    
neuron_func_2()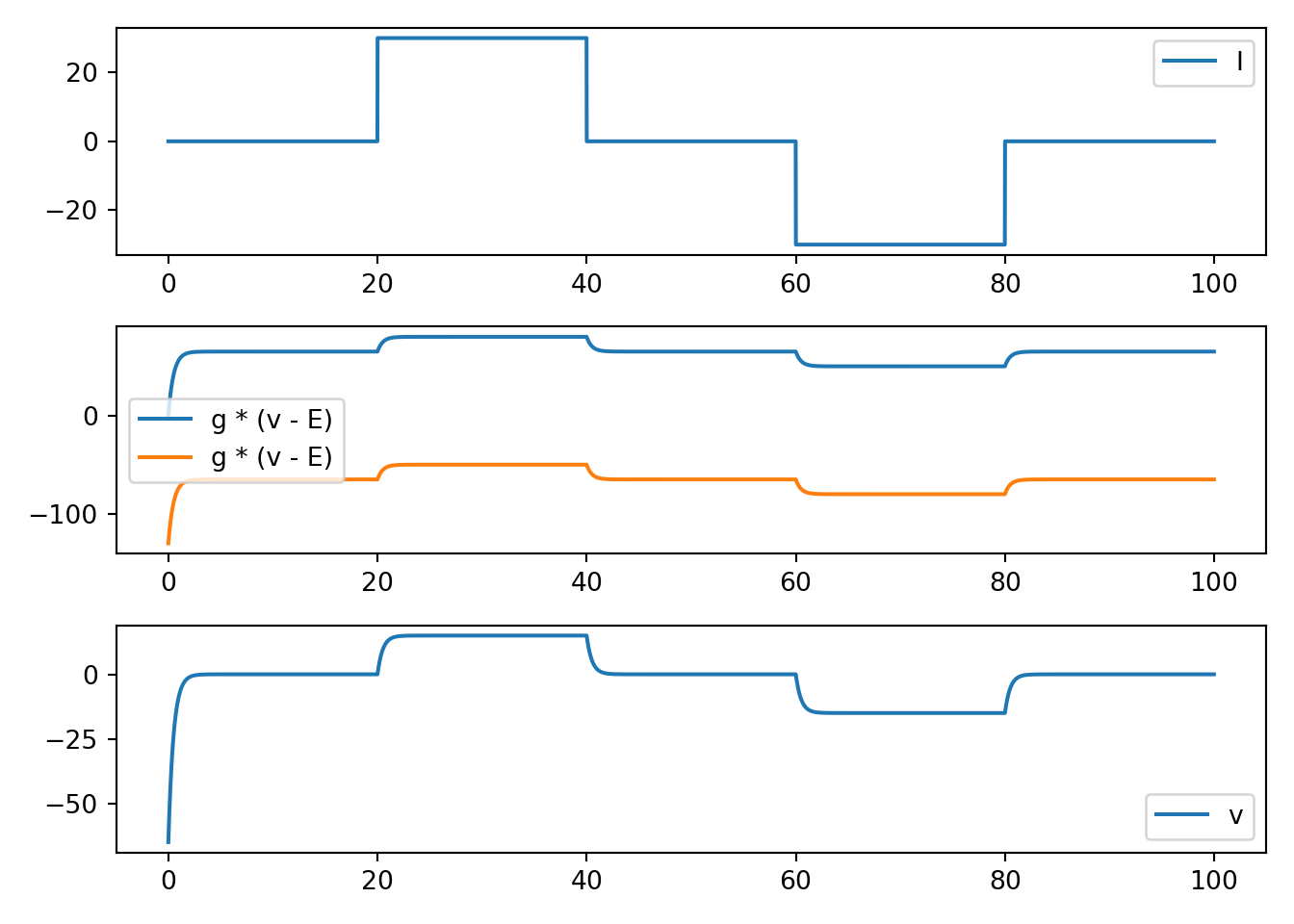

7.3 neuron_func_3

def neuron_func_3():
    '''
    dvdt = I - g_a_max * a * (v - E_a) - g_b * (v - E_b)
    dadt = (a_inf - a) / a_tau
    - Increase due to I can be amplified
    - rise looks an action potential
    - no fall back to rest
    '''

    def g_func_inf(v):
        # sigmoid shape
        return 1 / (1 + 0.1 * np.exp(-0.1 * (v)))

    def g_func_tau(v):
        # bell shape
        mu = -10.0
        sig = 50.0
        return np.exp(-((v - mu) / sig)**2)

    tau = 0.01
    T = 100
    t = np.arange(0, T, tau)
    n = t.shape[0]

    I = np.zeros(n)
    v = np.zeros(n)
    g_a = np.zeros(n)
    g_b = np.zeros(n)

    vr = -65.0

    E_a = -65.0
    E_b = -65.0

    g_a_max = 20.0
    g_b = 1.0

    C = 1.0

    v[0] = vr
    g_a[0] = g_func_inf(vr)

    I[n // 5:2 * n // 5] = 30.0
    I[3 * n // 5:4 * n // 5] = -30.0

    for i in range(1, n):
        delta_t = t[i] - t[i - 1]

        dvdt = (I[i - 1] - g_a_max * g_a[i - 1] * (v[i - 1] - E_a) - g_b *
                (v[i - 1] - E_b)) / C
        dgdt = (g_func_inf(v[i - 1]) - g_a[i - 1]) / g_func_tau(v[i - 1])

        v[i] = v[i - 1] + dvdt * delta_t
        g_a[i] = g_a[i - 1] + dgdt * delta_t

    fig, ax = plt.subplots(5, 1, squeeze=False)
    x = np.arange(-90, 90, 0.01)
    ax[0, 0].plot(x, g_func_inf(x), label='g_func_inf')
    ax[1, 0].plot(x, g_func_tau(x), label='g_func_tau')
    ax[2, 0].plot(t, I, label='I')
    ax[3, 0].plot(t,
                  g_a_max * g_a * (v - E_a),
                  label='g_max * g_a * (v - E_a)')
    ax[3, 0].plot(t, g_b * (v - E_b), label='g_b * (v - E_b)')
    ax[4, 0].plot(t, v, label='v')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()

neuron_func_3()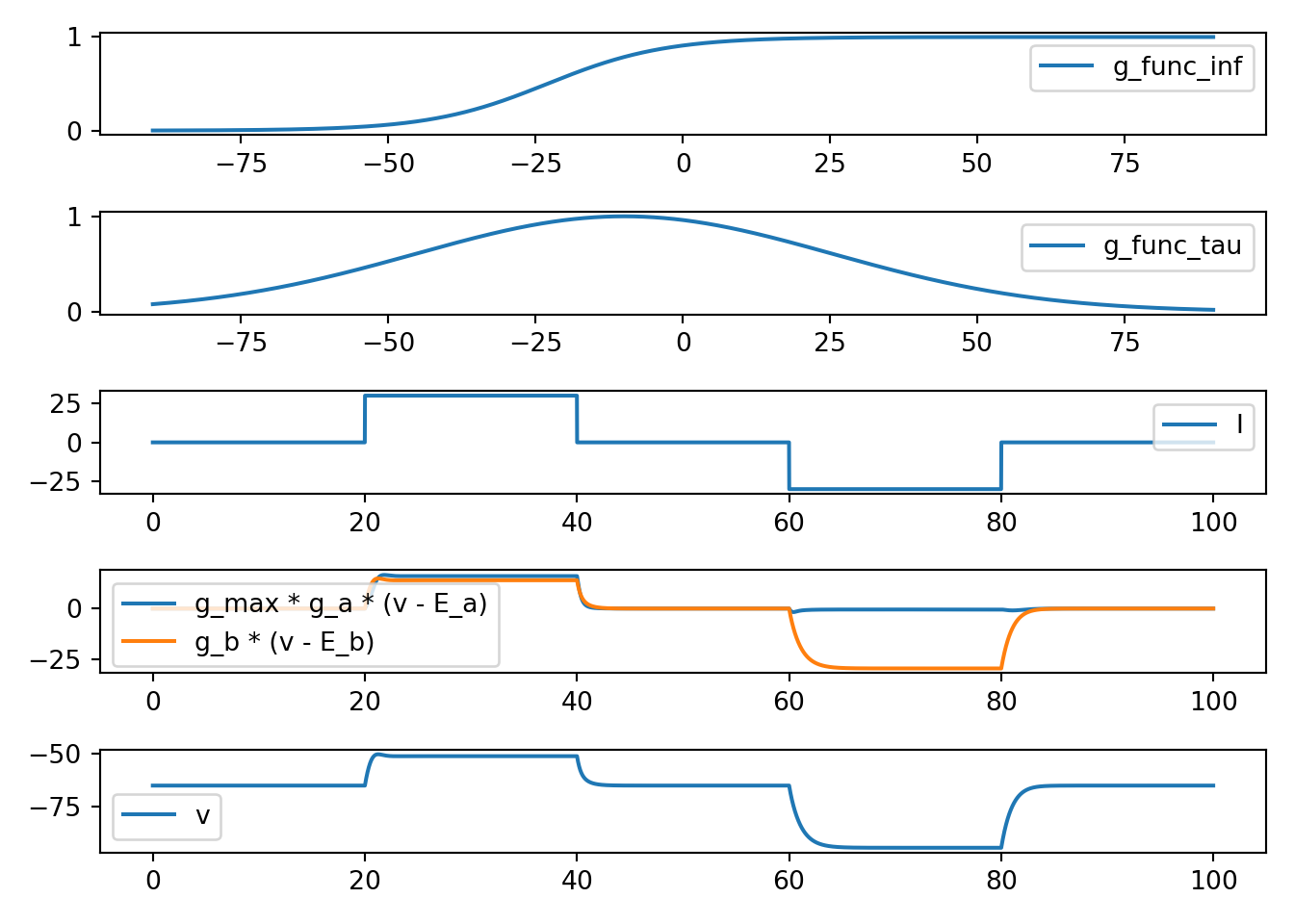

7.4 neuron_func_4

def neuron_func_4():
    '''
    dvdt = I - g_a_max * a * (v - E_a) - g_b_max * b * (v - E_b)
    dadt = (a_inf - a) / a_tau
    dbdt = (b_inf - b) / b_tau
    - Increase due to I can be amplified
    - rise looks an action potential (due to a)
    - can get a fall back to E_b (due to b)
    - fall occurs too slowly to be a normal action potential
    '''

    def g_func_inf_a(v):
        # sigmoid shape
        return 1 / (1 + 0.1 * np.exp(-0.1 * (v)))

    def g_func_inf_b(v):
        # sigmoid shape
        return -1 / (1.1 + 0.1 * np.exp(-0.1 * (v))) + 1

    def g_func_tau_a(v):
        # bell shape
        mu = -10.0
        sig = 60.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    def g_func_tau_b(v):
        # bell shape
        mu = -10.0
        sig = 50.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    tau = 0.01
    T = 200
    t = np.arange(0, T, tau)
    n = t.shape[0]

    I = np.zeros(n)
    v = np.zeros(n)
    g_a = np.zeros(n)
    g_b = np.zeros(n)

    vr = -65.0

    E_a = 120.0
    E_b = -70.0

    g_a_max = 1.0
    g_b_max = 2.0

    C = 1.0

    v[0] = vr
    g_a[0] = g_func_inf_a(vr)
    g_b[0] = g_func_inf_b(vr)

    I[n // 5:2 * n // 5] = 30.0
    I[3 * n // 5:4 * n // 5] = -30.0

    for i in range(1, n):
        delta_t = t[i] - t[i - 1]

        dvdt = (I[i - 1] - g_a_max * g_a[i - 1] *
                (v[i - 1] - E_a) - g_b_max * g_b[i - 1] * (v[i - 1] - E_b)) / C
        dgdt_a = (g_func_inf_a(v[i - 1]) - g_a[i - 1]) / g_func_tau_a(v[i - 1])
        dgdt_b = (g_func_inf_b(v[i - 1]) - g_b[i - 1]) / g_func_tau_b(v[i - 1])

        v[i] = v[i - 1] + dvdt * delta_t
        g_a[i] = g_a[i - 1] + dgdt_a * delta_t
        g_b[i] = g_b[i - 1] + dgdt_b * delta_t

    fig, ax = plt.subplots(5, 1, squeeze=False)
    x = np.arange(-90, 90, 0.01)
    ax[0, 0].plot(x, g_func_inf_a(x), label='g_func_inf_a')
    ax[0, 0].plot(x, g_func_inf_b(x), label='g_func_inf_b')
    ax[1, 0].plot(x, g_func_tau_a(x), label='g_func_tau_a')
    ax[1, 0].plot(x, g_func_tau_b(x), label='g_func_tau_b')
    ax[2, 0].plot(t, I, label='I')
    ax[3, 0].plot(t,
                  g_a_max * g_a * (v - E_a),
                  label='g_a_max * g_a * (v - E_a)')
    ax[3, 0].plot(t,
                  g_b_max * g_b * (v - E_b),
                  label='g_b_max * g_b * (v - E_b)')
    ax[4, 0].plot(t, v, label='v')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()

neuron_func_4()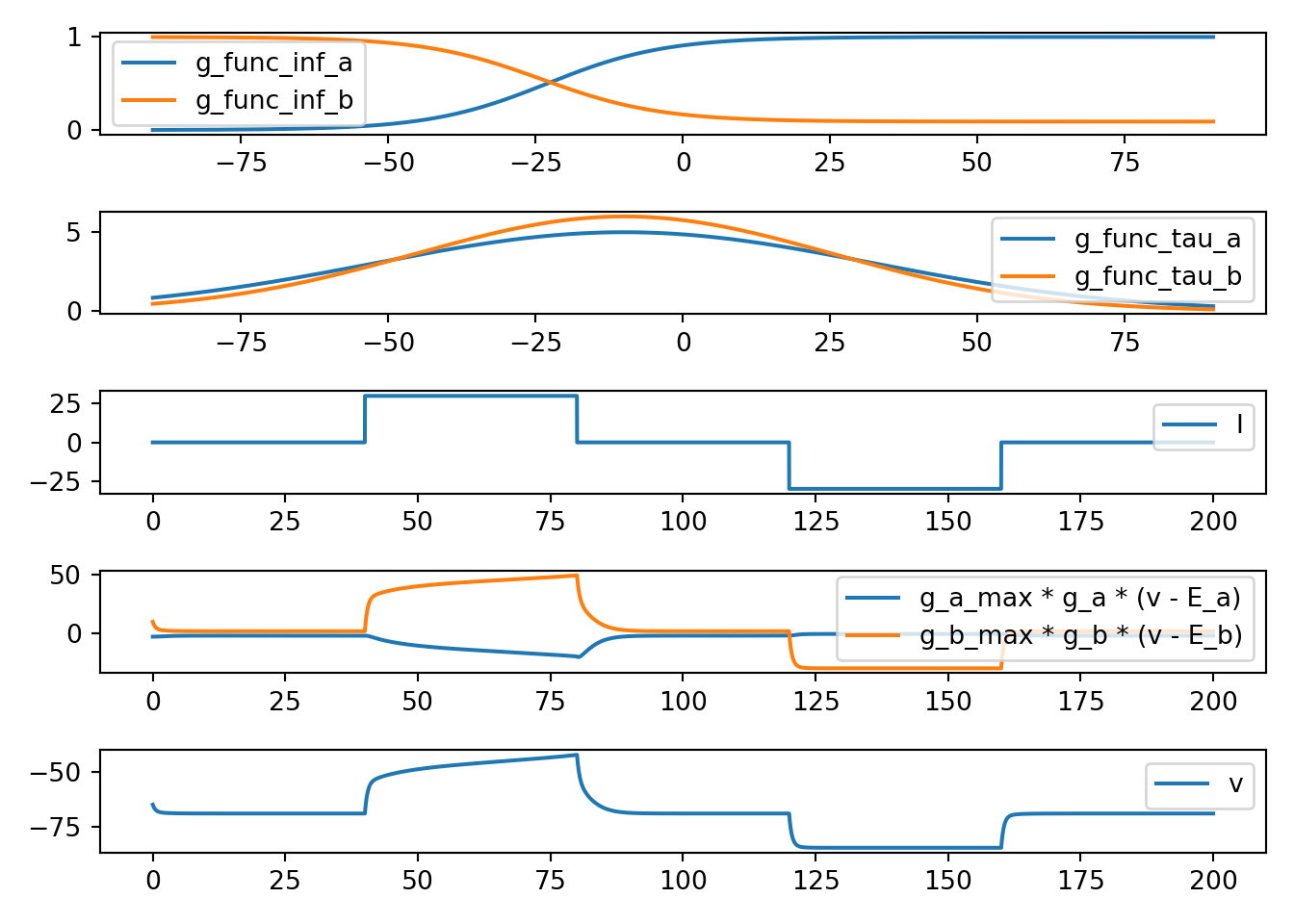

7.5 neuron_func_5

def neuron_func_5():
    '''
    dvdt = I - g_a_max * a_act**3 * a_inact * (v - E_a) - g_b * (v - E_b)
    dadt_act = (a_act_inf - a_act) / a_act_tau
    dadt_inact = (a_inact_inf - a_inact) / a_inact_tau
    - Increase due to I can be amplified
    - rise looks an action potential (due to a_act)
    - fall back to E_b (due to a_inact)
    - still not quite right... but why really?
    '''

    def g_func_inf_a_act(v):
        # sigmoid shape
        return 1 / (1 + 0.1 * np.exp(-0.5 * (v + 50.0)))

    def g_func_inf_a_inact(v):
        # sigmoid shape
        return -1 / (1.1 + 0.1 * np.exp(-0.1 * (v))) + 1

    def g_func_tau_a_act(v):
        # bell shape
        mu = -10.0
        sig = 60.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    def g_func_tau_a_inact(v):
        # bell shape
        mu = -10.0
        sig = 50.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    tau = 0.01
    T = 200
    t = np.arange(0, T, tau)
    n = t.shape[0]

    I = np.zeros(n)
    v = np.zeros(n)
    g_a_act = np.zeros(n)
    g_a_inact = np.zeros(n)

    vr = -65.0

    E_a = 120.0
    E_b = -70.0

    g_a_max = 2.0
    g_b_max = 1.0

    C = 1.0

    v[0] = vr
    g_a_act[0] = g_func_inf_a_act(vr)
    g_a_inact[0] = g_func_inf_a_inact(vr)

    I[n // 5:2 * n // 5] = 30.0
    I[3 * n // 5:4 * n // 5] = -30.0

    for i in range(1, n):
        delta_t = t[i] - t[i - 1]

        dvdt = (I[i - 1] - g_a_max * g_a_act[i - 1]**3 * g_a_inact[i - 1] *
                (v[i - 1] - E_a) - g_b_max * (v[i - 1] - E_b)) / C
        dgdt_a_act = (g_func_inf_a_act(v[i - 1]) -
                      g_a_act[i - 1]) / g_func_tau_a_act(v[i - 1])
        dgdt_a_inact = (g_func_inf_a_inact(v[i - 1]) -
                        g_a_inact[i - 1]) / g_func_tau_a_inact(v[i - 1])

        v[i] = v[i - 1] + dvdt * delta_t
        g_a_act[i] = g_a_act[i - 1] + dgdt_a_act * delta_t
        g_a_inact[i] = g_a_inact[i - 1] + dgdt_a_inact * delta_t

    fig, ax = plt.subplots(5, 1, squeeze=False)
    x = np.arange(-90, 90, 0.01)
    ax[0, 0].plot(x, g_func_inf_a_act(x), label='g_func_inf_a_act')
    ax[0, 0].plot(x, g_func_inf_a_inact(x), label='g_func_inf_a_inact')
    ax[1, 0].plot(x, g_func_tau_a_act(x), label='g_func_tau_a_act')
    ax[1, 0].plot(x, g_func_tau_a_inact(x), label='g_func_tau_a_inact')
    ax[2, 0].plot(t, I, label='I')
    ax[3, 0].plot(t,
                  g_a_max * g_a_act * (v - E_a),
                  label='g_a_max * g_a_act * (v - E_a)')
    ax[3, 0].plot(t,
                  g_a_max * g_a_inact * (v - E_a),
                  label='g_a_max * g_a_inact * (v - E_a)')
    ax[4, 0].plot(t, v, label='v')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()
    
neuron_func_5()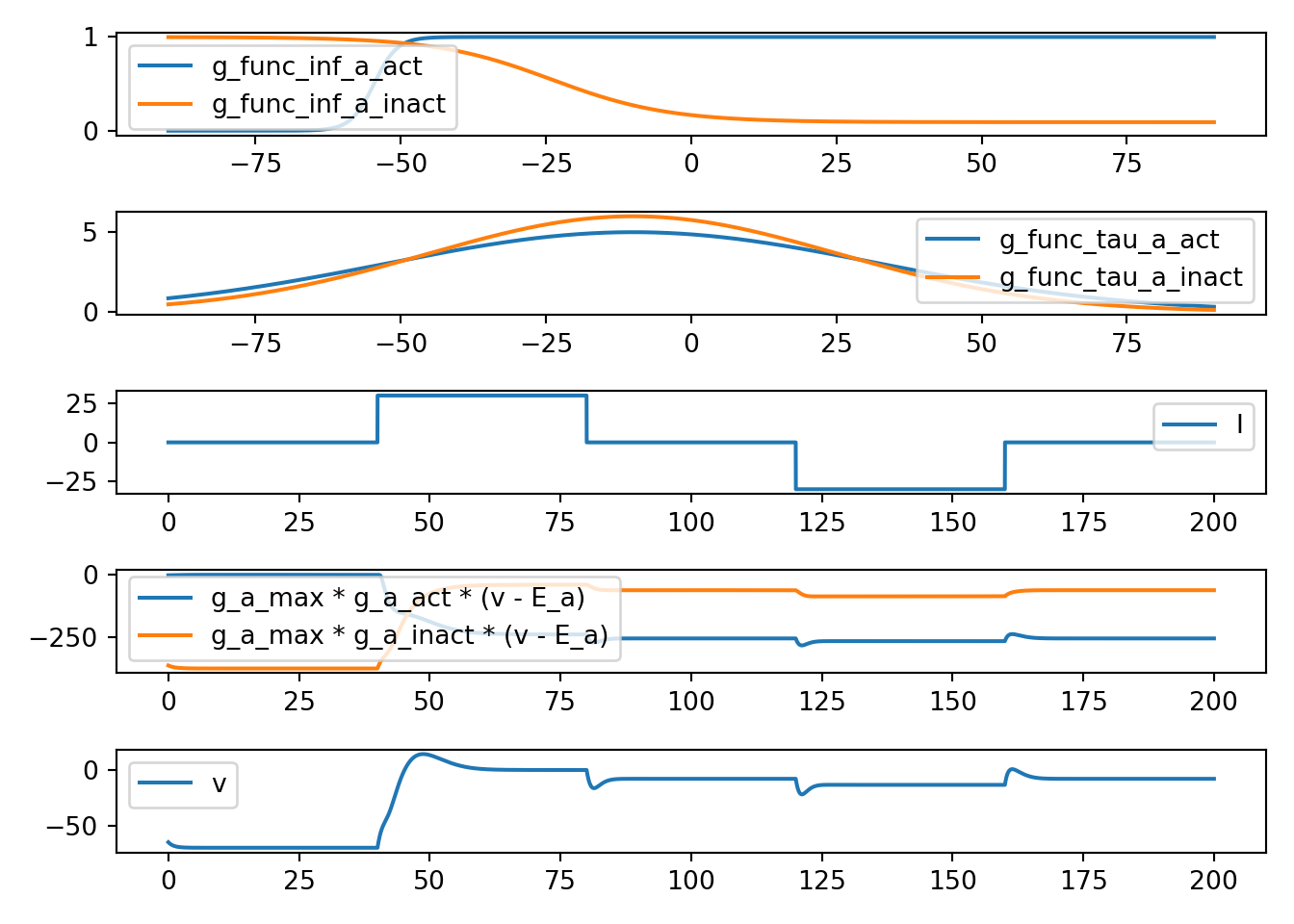

7.6 neuron_func_6

def neuron_func_6():
    '''
    dvdt = I - g_a_max * a_act**3 * a_inact * (v - E_a) - g_b_max * b * (v - E_b)
    dadt_act = (a_act_inf - a_act) / a_act_tau
    dadt_inact = (a_inact_inf - a_inact) / a_inact_tau
    dbdt = (b_inf - b) / b_tau
    - Increase due to I can be amplified
    - rise looks an action potential (due to a_act)
    - fall back to E_b (due to a_inact and due to b)
    - looking prettty good presumably
    '''

    def g_func_inf_a_act(v):
        # sigmoid shape
        return 1 / (1 + 0.1 * np.exp(-0.5 * (v + 50.0)))

    def g_func_inf_a_inact(v):
        # sigmoid shape
        return -1 / (1.1 + 0.1 * np.exp(-0.1 * (v))) + 1

    def g_func_inf_b(v):
        # sigmoid shape
        return 1 / (1.1 + 0.1 * np.exp(-0.09 * (v)))

    def g_func_tau_a_act(v):
        # bell shape
        mu = -10.0
        sig = 60.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    def g_func_tau_a_inact(v):
        # bell shape
        mu = -10.0
        sig = 50.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    def g_func_tau_b(v):
        # bell shape
        mu = 5.0
        sig = 50.0
        return (300 / sig) * np.exp(-((v - mu) / sig)**2)

    tau = 0.01
    T = 200
    t = np.arange(0, T, tau)
    n = t.shape[0]

    I = np.zeros(n)
    v = np.zeros(n)
    g_a_act = np.zeros(n)
    g_a_inact = np.zeros(n)
    g_b = np.zeros(n)

    vr = -65.0

    E_a = 120.0
    E_b = -70.0

    g_a_max = 2.0
    g_b_max = 5.0

    C = 1.0

    v[0] = vr
    g_a_act[0] = g_func_inf_a_act(vr)
    g_a_inact[0] = g_func_inf_a_inact(vr)
    g_b[0] = g_func_inf_b(vr)

    I[n // 5:2 * n // 5] = 30.0
    I[3 * n // 5:4 * n // 5] = -30.0

    for i in range(1, n):
        delta_t = t[i] - t[i - 1]

        dvdt = (I[i - 1] - g_a_max * g_a_act[i - 1]**3 * g_a_inact[i - 1] *
                (v[i - 1] - E_a) - g_b_max * g_b[i - 1]**4 *
                (v[i - 1] - E_b)) / C
        dgdt_a_act = (g_func_inf_a_act(v[i - 1]) -
                      g_a_act[i - 1]) / g_func_tau_a_act(v[i - 1])
        dgdt_a_inact = (g_func_inf_a_inact(v[i - 1]) -
                        g_a_inact[i - 1]) / g_func_tau_a_inact(v[i - 1])
        dgdt_b = (g_func_inf_b(v[i - 1]) - g_b[i - 1]) / g_func_tau_b(v[i - 1])

        v[i] = v[i - 1] + dvdt * delta_t
        g_a_act[i] = g_a_act[i - 1] + dgdt_a_act * delta_t
        g_a_inact[i] = g_a_inact[i - 1] + dgdt_a_inact * delta_t
        g_b[i] = g_b[i - 1] + dgdt_b * delta_t

    fig, ax = plt.subplots(5, 1, squeeze=False)
    x = np.arange(-90, 90, 0.01)
    ax[0, 0].plot(x, g_func_inf_a_act(x), label='g_func_inf_a_act')
    ax[0, 0].plot(x, g_func_inf_a_inact(x), label='g_func_inf_a_inact')
    ax[0, 0].plot(x, g_func_inf_b(x), label='g_func_inf_b')
    ax[1, 0].plot(x, g_func_tau_a_act(x), label='g_func_tau_a_act')
    ax[1, 0].plot(x, g_func_tau_a_inact(x), label='g_func_tau_a_inact')
    ax[1, 0].plot(x, g_func_tau_b(x), label='g_func_tau_b')
    ax[2, 0].plot(t, I, label='I')
    ax[3, 0].plot(t,
                  g_a_max * g_a_act * (v - E_a),
                  label='g_a_max * g_a_act * (v - E_a)')
    ax[3, 0].plot(t,
                  g_a_max * g_a_inact * (v - E_a),
                  label='g_a_max * g_a_inact * (v - E_a)')
    ax[3, 0].plot(t,
                  g_b_max * g_b * (v - E_b),
                  label='g_b_max * g_b * (v - E_b)')
    ax[4, 0].plot(t, v, label='v')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()
    
neuron_func_6()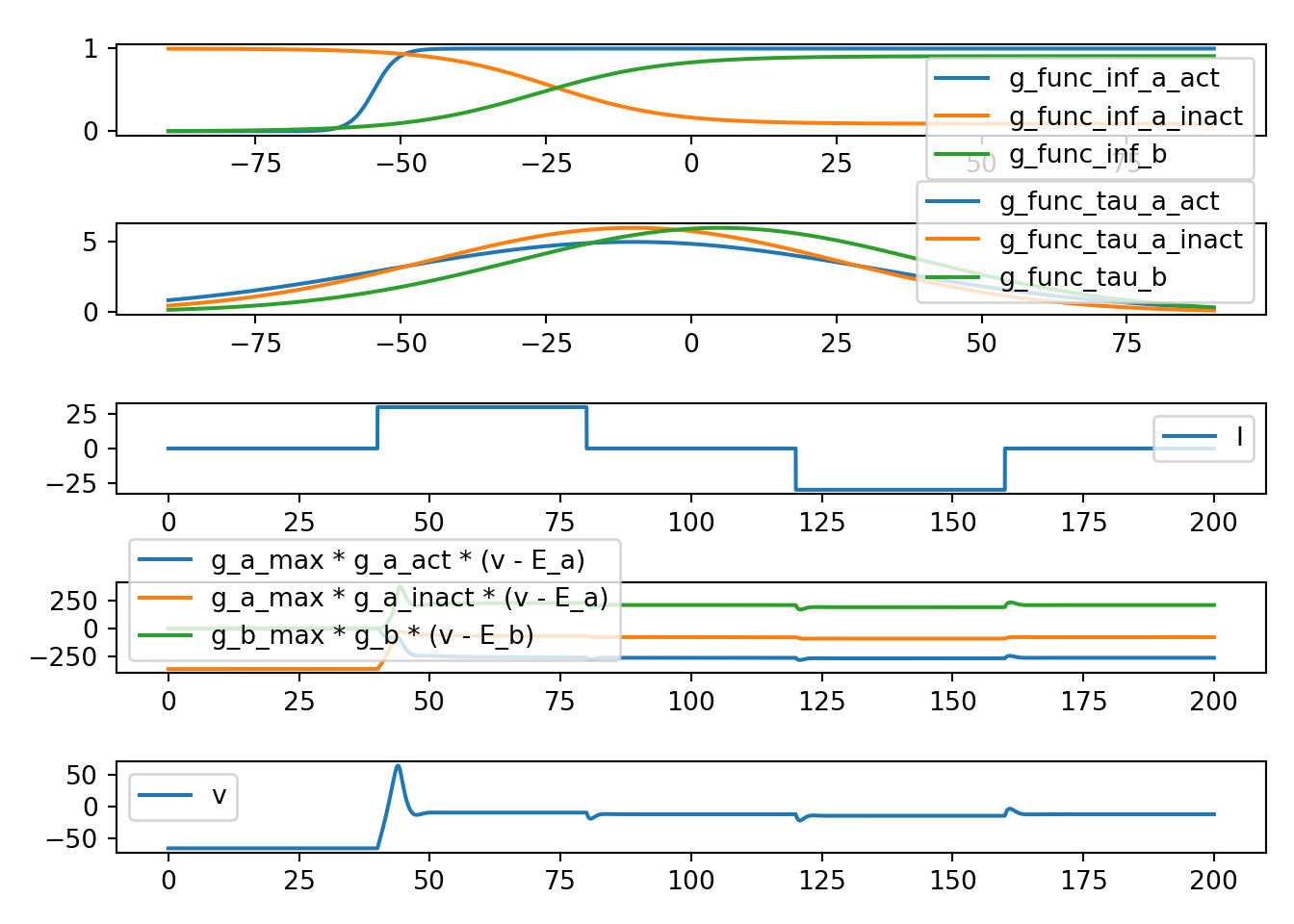

7.7 neuron_func_7

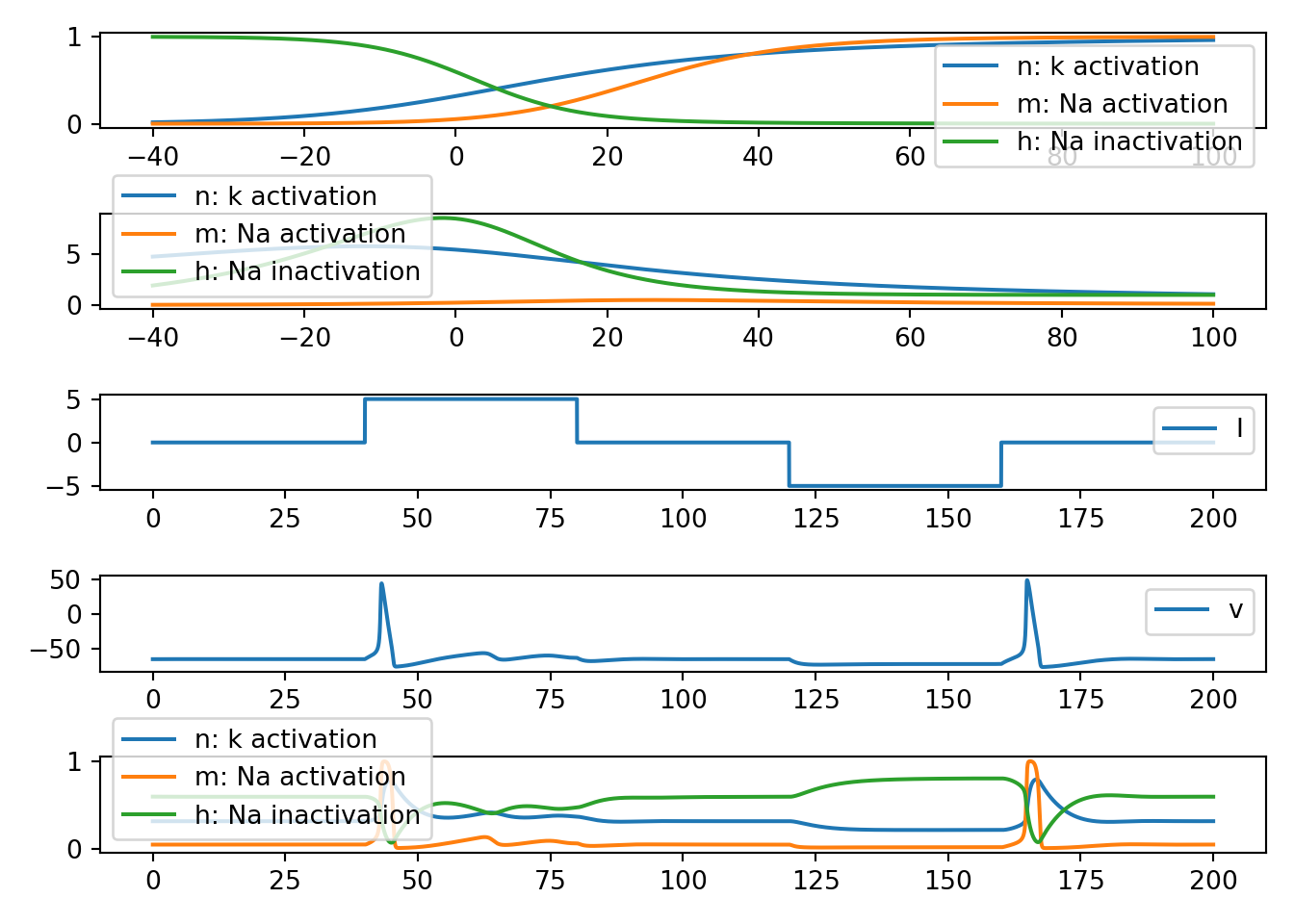
def neuron_func_7():
    '''
    NOTE: Full HH
    '''

    # NOTE: n gating variables
    def n_inf(v):
        return alpha_func_n(v) / (alpha_func_n(v) + beta_func_n(v))

    def n_tau(v):
        return 1.0 / (alpha_func_n(v) + beta_func_n(v))

    def alpha_func_n(v):
        return 0.01 * (10.0 - v) / (np.exp((10.0 - v) / 10.0) - 1.0)

    def beta_func_n(v):
        return 0.125 * np.exp(-v / 80.0)

    # NOTE: m gating variables
    def m_inf(v):
        return alpha_func_m(v) / (alpha_func_m(v) + beta_func_m(v))

    def m_tau(v):
        return 1.0 / (alpha_func_m(v) + beta_func_m(v))

    def alpha_func_m(v):
        return 0.1 * (25.0 - v) / (np.exp((25.0 - v) / 10.0) - 1.0)

    def beta_func_m(v):
        return 4.0 * np.exp(-v / 18.0)

    # NOTE: h gating variables
    def h_inf(v):
        return alpha_func_h(v) / (alpha_func_h(v) + beta_func_h(v))

    def h_tau(v):
        return 1.0 / (alpha_func_h(v) + beta_func_h(v))

    def alpha_func_h(v):
        return 0.07 * np.exp(-v / 20.0)

    def beta_func_h(v):
        return 1.0 / (np.exp((30.0 - v) / 10.0) + 1.0)

    # NOTE: simulation parameter etc
    tau = 0.01
    T = 200
    t = np.arange(0, T, tau)
    nn = t.shape[0]

    I = np.zeros(nn)
    v = np.zeros(nn)
    n = np.zeros(nn)
    m = np.zeros(nn)
    h = np.zeros(nn)

    vr = -65.0

    v[0] = vr
    n[0] = n_inf(vr*0)
    m[0] = m_inf(vr*0)
    h[0] = h_inf(vr*0)

    g_k = 36.0
    g_na = 120.0
    g_leak = 0.30

    E_k = -12 + vr
    E_na = 120 + vr
    E_leak = 10.6 + vr

    C = 1.0

    I[nn // 5:2 * nn // 5] = 5.0
    I[3 * nn // 5:4 * nn // 5] = -5.0

    # NOTE: Euler's method simulation
    for i in range(1, nn):
        delta_t = t[i] - t[i - 1]

        I_k = g_k * (n[i - 1]**4) * (v[i - 1] - E_k)
        I_na = g_na * (m[i - 1]**3) * (h[i - 1]) * (v[i - 1] - E_na)
        I_leak = g_leak * (v[i - 1] - E_leak)

        dvdt = (I[i - 1] - (I_k + I_na + I_leak)) / C

        dndt = (n_inf(v[i - 1] - vr) - n[i - 1]) / n_tau(v[i - 1] - vr)
        dmdt = (m_inf(v[i - 1] - vr) - m[i - 1]) / m_tau(v[i - 1] - vr)
        dhdt = (h_inf(v[i - 1] - vr) - h[i - 1]) / h_tau(v[i - 1] - vr)

        v[i] = v[i - 1] + dvdt * delta_t
        n[i] = n[i - 1] + dndt * delta_t
        m[i] = m[i - 1] + dmdt * delta_t
        h[i] = h[i - 1] + dhdt * delta_t

    # NOTE: inspect gating functions
    fig, ax = plt.subplots(5, 1, squeeze=False)
    
    v_range = np.arange(-40, 100, 0.01)
    
    ax[0, 0].plot(v_range, n_inf(v_range), label='n: k activation')
    ax[0, 0].plot(v_range, m_inf(v_range), label='m: Na activation')
    ax[0, 0].plot(v_range, h_inf(v_range), label='h: Na inactivation')
    ax[1, 0].plot(v_range, n_tau(v_range), label='n: k activation')
    ax[1, 0].plot(v_range, m_tau(v_range), label='m: Na activation')
    ax[1, 0].plot(v_range, h_tau(v_range), label='h: Na inactivation')
    ax[2, 0].plot(t, I, label='I')
    ax[3, 0].plot(t, v, label='v')
    ax[4, 0].plot(t, n, label='n: k activation')
    ax[4, 0].plot(t, m, label='m: Na activation')
    ax[4, 0].plot(t, h, label='h: Na inactivation')
    [x.legend() for x in ax.flatten()]
    plt.tight_layout()
    plt.show()
    
neuron_func_7()